What is a Zero-Coupon Yield Curve (Spot Curve)? The essential Rate for Discounting

What is the Zero-Coupon Yield Curve?

The Zero-Coupon Yield Curve (often called the "spot curve" or "zero curve") is a graphical representation of the yield or “spot rate” that you would earn on a single, lump-sum payment at a specific future maturity, assuming no intermediate payments.

• Unlike a standard yield curve, which plots the yields of coupon-paying instruments (like standard 10-year Treasuries or Gilts), the Zero-Coupon curve represents the "pure" interest rate for a specific time horizon. It strips away the distortion caused by intermediate coupon payments, showing the true yield an investor would earn if they locked in their money today and received a single lump sum at maturity.
• While it’s rarely directly observable in the market, the curve is mathematically derived from the prices of highly liquid instruments, including government bonds and overnight index swaps. Below is a graph of a Zero-Coupon yield curve for US government bonds.

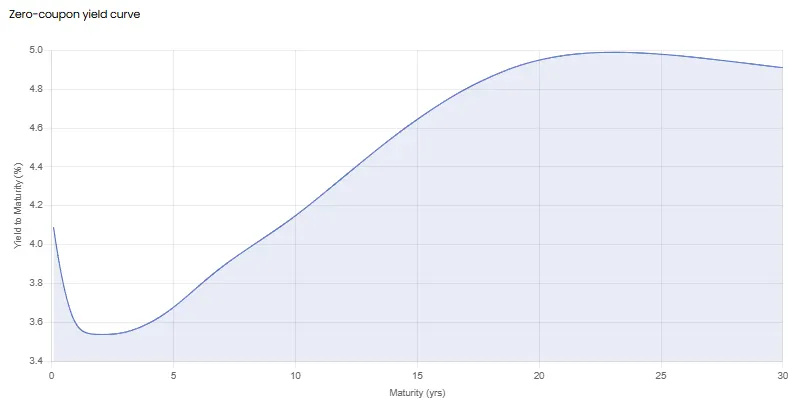
Where to access Zero-Coupon Yield Curves? We offer Zero-Coupon Bond Yield Curve data for Government Bonds and Reference Rates like SOFR, SONIA, CORRA and ESTR. No need to calculate it yourself.

You can access and embed the zero rates into your workflows in two primary ways:

1. API Integration: Embed the latest zero rates directly into your treasury systems or software
2. Excel Add-in: Pull real-time zero rates into your spreadsheet models using a simple, native function.

You can also access them via our Web App. Sign up for a 14-Day free Trial and navigate to the Government Bond Section of our platform to download the Zero-Coupon Bond Yield Curve of your choice.

What is the Zero-Coupon Curve used for?

The Zero-Coupon curve is the fundamental building block for modern financial valuation. Its "pure" nature makes it essential for pricing complex instruments that standard yield curves cannot handle accurately.

Its primary uses include:

• Discounting Cash Flows and Present Value Calculations:

It provides the unique discount rate required for each specific cash flow date of a security. This is required for calculating the PV of a future payment C

The discount factor D(T) is derived directly from the spot rate S(T)

This is the basis for pricing instruments like interest rate swaps, Forward Rate Agreements (FRAs), options, and structured products

• Constructing the Forward Curve:

One of its most important applications is acting as the mathematical foundation and main component in constructing the Forward Curve, which we specialise in offering. While the Zero-Coupon curve tells you the rate for a loan starting today, the forward curve implies what the rate would be for a loan starting in the future. These are important rates used in risk management and forecasting debt service costs.

Par vs. Swap vs. Spot vs. Forward Curve

For financial modelling the word “curve” is not singular; there are several different types of curve defined by the underlying market and the choice depends on the use-case. Below we show a comparison of the different curves along with examples of BlueGamma functions, available via our Excel Add-In.

How is the Zero-Coupon Curve Constructed?

Constructing a Zero-Coupon curve is an advanced financial modelling task. Since "pure" Zero-Coupon instruments don't exist for every maturity, we must reverse-engineer the curve from coupon-bearing bonds using a method called Bootstrapping.

The basic steps are:

1. Gather Data: Collect market prices for a set of liquid instruments (e.g. swaps, FRAs, futures).
2. Anchor the Curve: Use short-term Zero-Coupon instruments to set the initial rates.
3. Iterative Solving (Bootstrap): Move to the next longest instrument (e.g. a swap). We discount all known intermediate cash flows using the already solved rates. Then algebraically solve for the single unknown zero-rate.
4. Repeat: Use the newly found rates to solve for the next maturity, stepping forward year by year until the curve is complete.

This process requires rigorous data cleaning and interpolation methods (like Cubic Spline or Nelson-Siegel) to ensure the curve is smooth and arbitrage-free.

Where can I download Zero-Coupon Bond Yield Curves?

Because Zero-Coupon yields are not directly observable for all maturities, you cannot simply "look them up" on a standard exchange; they must be calculated using the complex bootstrapping methods described above, built from market rates (like OIS, Futures and Swaps).

Most teams choose not to build these models in-house due to the risk of data errors and the maintenance required to keep the curves smooth and accurate.

You can access the Zero-Coupon curve of your choice either via our Platform, Excel add-in or API.

To gain access to our platform Sign up for a 14-Day free Trial

Zero-Coupon Yield Curve API

If you want to pull the Zero-Coupon Yield Curve via API, request API access by filling out this form or by talking to our sales team via the chat.

Here’s the API docs for our Zero Rates endpoint and an example of how to do it in Python:

pip install requests pandas matplotlib seaborn

import requests
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# ---------------------------------------------------------
# Configuration
# ---------------------------------------------------------
API_KEY = "YOUR-API-KEY"  # Replace with your API key
BASE_URL = "https://api.bluegamma.io/v1/zero_rate"

# The specific points (tenors) we want to plot on the curve
TENORS_TO_FETCH = [
    "1M", "3M", "6M", "9M", 
    "1Y", "2Y", "3Y", "4Y", "5Y", 
    "7Y", "10Y", "15Y", "20Y", "30Y"
]

def fetch_sofr_zero_curve():
    """
    Loops through defined tenors and fetches the zero rate for each
    using the BlueGamma /zero_rate endpoint.
    """
    curve_data = []
    
    headers = {
        "x-api-key": API_KEY,
        "Accept": "application/json"
    }

    print(f"Fetching {len(TENORS_TO_FETCH)} data points for SOFR Zero Curve...")

    for tenor in TENORS_TO_FETCH:
        # Parameters for the API call
        params = {
            "index": "SOFR",
            "date": tenor,                  # The API accepts tenors here (e.g., "1Y")
            "compounding": "Continuous",    # Continuous compounding is standard for zero curves
            "day_count": "Actual360"        # Standard money market convention
        }

        try:
            response = requests.get(BASE_URL, params=params, headers=headers)
            
            if response.status_code == 200:
                data = response.json()
                
                # Store the result
                curve_data.append({
                    "Tenor": tenor,
                    "Maturity Date": data['date'],       # The calculated maturity date provided by API
                    "Zero Rate (%)": data['zero_rate']   # The rate value
                })
                print(f"✔ {tenor}: {data['zero_rate']}%")
                
            else:
                print(f"✖ {tenor}: Failed ({response.status_code}) - {response.text}")

        except Exception as e:
            print(f"Error fetching {tenor}: {e}")

    return pd.DataFrame(curve_data)

def plot_curve(df):
    """
    Visualizes the dataframe using Matplotlib/Seaborn
    """
    if df.empty:
        print("No data available to plot.")
        return

    # Ensure dates are datetime objects for proper sorting and plotting
    df['Maturity Date'] = pd.to_datetime(df['Maturity Date'])
    df = df.sort_values(by='Maturity Date')

    # Setup Plot
    plt.figure(figsize=(12, 6))
    sns.set_style("whitegrid")

    # Draw the line and the points
    plt.plot(df['Maturity Date'], df['Zero Rate (%)'],
             linestyle='-', linewidth=2, color="#48a8f7", label='SOFR Zero Rate (Continuous)')

    # Formatting
    plt.title('SOFR Zero Coupon Curve', fontsize=16, pad=15)
    plt.xlabel('Maturity Date', fontsize=12)
    plt.ylabel('Zero Rate (%)', fontsize=12)
    plt.legend()
    
    # Rotate x-axis dates for better readability
    plt.gcf().autofmt_xdate()
    
    plt.tight_layout()
    plt.show()

if __name__ == "__main__":
    # 1. Fetch Data
    df = fetch_sofr_zero_curve()
    
    # 2. Display Data Table
    if not df.empty:
        print("\n--- Curve Data ---")
        print(df[['Tenor', 'Maturity Date', 'Zero Rate (%)']].to_string(index=False))
        
        # 3. Plot Data
        plot_curve(df)

Terminal Output:

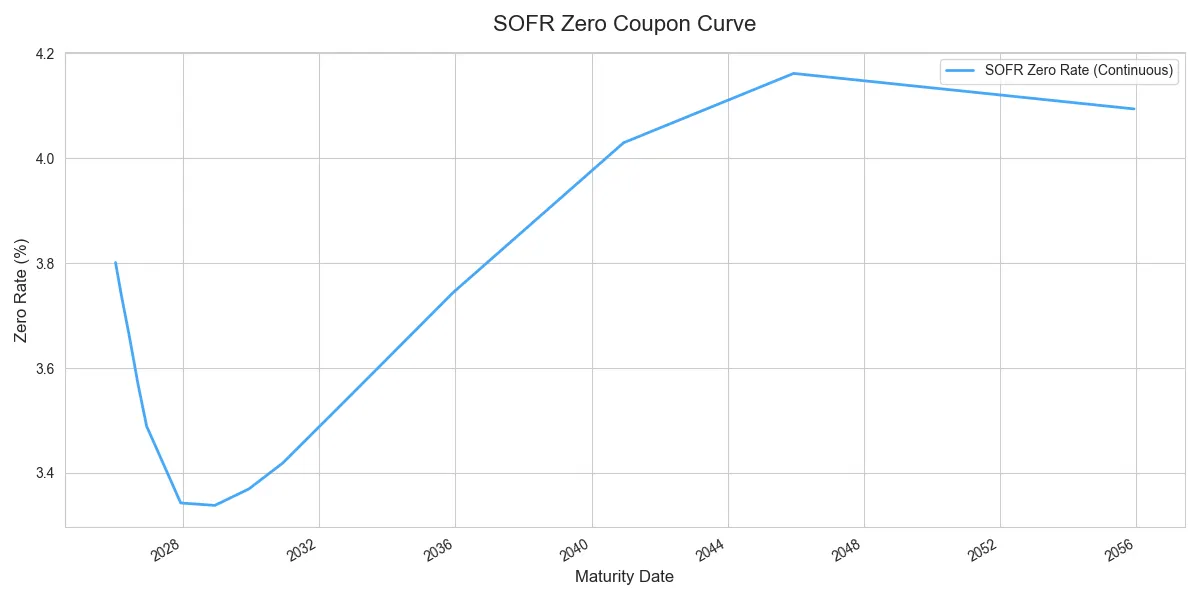
-- Curve Data ---

Tenor Maturity Date Zero Rate (%)

1M 2026-01-08 3.801107

3M 2026-03-09 3.741141

6M 2026-06-08 3.657661

9M 2026-09-08 3.568376

1Y 2026-12-08 3.489558

2Y 2027-12-08 3.344095

3Y 2028-12-08 3.339697

4Y 2029-12-10 3.372122

5Y 2030-12-09 3.422622

7Y 2032-12-08 3.551917

10Y 2035-12-10 3.747098

15Y 2040-12-10 4.031899

20Y 2045-12-08 4.163288

30Y 2055-12-08 4.095526

Zero-Coupon Curve API Visualisation:

Other derived data points

Here are some of the other derived data points you might want to access: